有關 Barnsley Fern
前言
Barnsley Fern
引用英文版Wikipedia對Barnsley Fern的介紹:
The Barnsley fern is a fractal named after the British mathematician Michael Barnsley who first described it in his book Fractals Everywhere. From Wikipedia
翻譯成中文大概就是: “Barnsley Fern 是一個由一位英國數學家 Michael Barnsley 在他所寫的書 Fractals Everywhere 中所描述的一種碎形”
那甚麼是碎形呢? 我們再次引用Wikipedia,不過這次是中文版(我懶得翻譯阿)
碎形(英語:Fractal),又稱分形、殘形,通常被定義為「一個粗糙或零碎的幾何形狀,可以分成數個部分,且每一部分都(至少近似地)是整體縮小後的形狀」,即具有自相似的性質。From Wikipedia
有名的碎形有科赫雪花與謝爾賓斯基三角形,有關謝爾賓斯基三角形可以參考部落格的另外一篇文章 https://jayin92.github.io/posts/sierpinski-triangle/

科赫雪花

謝爾賓斯基三角形
我們可以很容易的看到說不管你把一個碎形放大多少倍,它所呈現的圖形會跟原本一模一樣,這就是碎形自相似的性質。
不過我們今天不會太深入去講碎形,因為其實我也不太會😭
Barnsley Fern 介紹
其實Barnsley Fern的描繪過程可以由下面方程組 (Transmotions functions “變換函數?”) 決定:
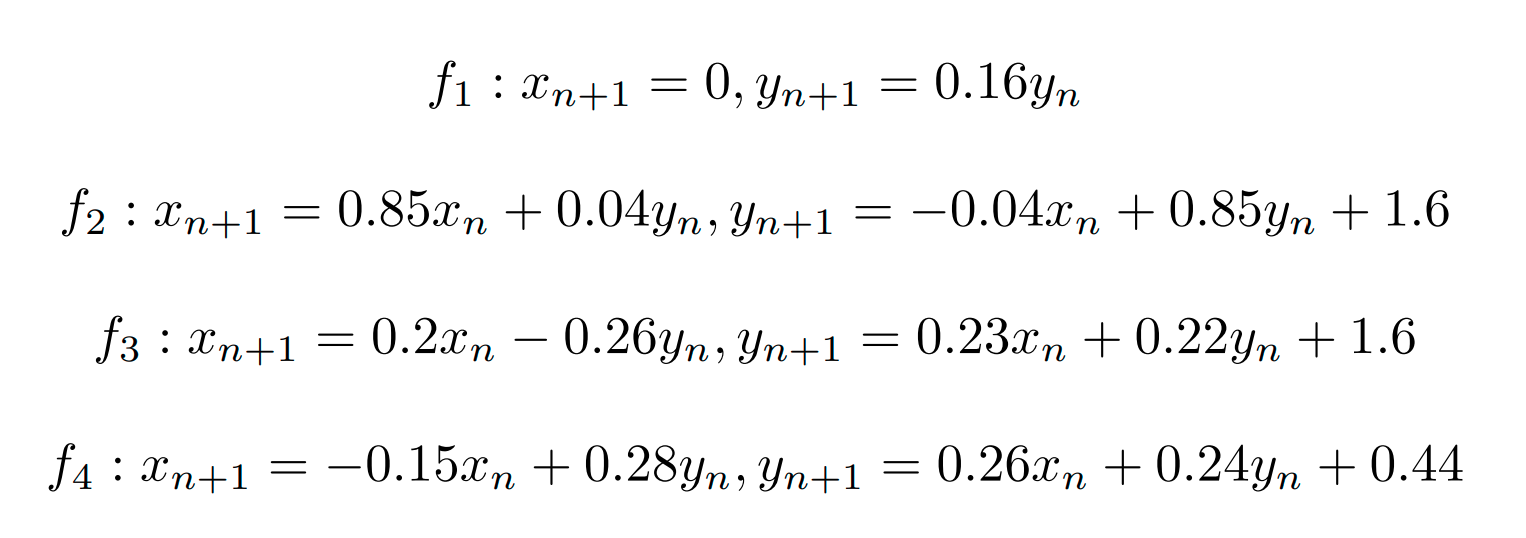
其中$P()$代表此方程式在此方程組的發生機率
而$f_1$主要生成Barnsley Fern中的梗的部分
$f_2$為小的散葉
$f_3$為左邊的葉子
$f_4$為右邊的葉子
利用Python內建的Turtle庫畫出Barnsley Fern
不過在電腦科學裡,我們可以利用迭代(遞迴)的方式來繪出Barnsley Fern

所以我們可以利用python寫出上面四個方程式 (函數傳入值及回傳值皆為tuple)
def f1(point): # 1%
x = point[0]
y = point[1]
x1 = 0
y1 = 0.16 * y
return (x1, y1)
def f2(point): # 85%
x = point[0]
y = point[1]
x1 = 0.85 * x + 0.04 * y
y1 = -0.04 * x + 0.85 * y + 1.6
return (x1, y1)
def f3(point): # 7%
x = point[0]
y = point[1]
x1 = 0.2 * x - 0.26 * y
y1 = 0.23 * x + 0.22 * y + 1.6
return (x1, y1)
def f4(point): # 7%
x = point[0]
y = point[1]
x1 = -0.15 * x + 0.28 * y
y1 = 0.26 * x + 0.24 * y + 0.44
return (x1, y1)
然後我們用一個非常沒有效率的方法來決定方程式的發生機率
choices = []
choices.append(1)
for i in range(85):
choices.append(2)
for i in range(7):
choices.append(3)
for i in range(7):
choices.append(4)
然後利用random來從choices隨機取出1,2,3,4四個值
while True:
print(i)
function = random.choice(choices)
print(function)
if function == 1:
tracepoint = f1(tracepoint)
drawdot(tracepoint)
elif function == 2:
tracepoint = f2(tracepoint)
drawdot(tracepoint)
elif function == 3:
tracepoint = f3(tracepoint)
drawdot(tracepoint)
elif function == 4:
tracepoint = f4(tracepoint)
drawdot(tracepoint)
print(tracepoint)
i += 1
drawdot 為利用turtle寫成的繪點函數 (回傳值及傳入值皆為tuple)
所以我們可以利用無限迴圈不斷迭代來繪出Barnsley Fern
這是畫出的結果

可以明顯看到這張圖是全部用點點出來的,謝爾賓斯基三角形也會利用類似方法產生。
參考資料
https://en.wikipedia.org/wiki/Barnsley_fern
https://en.wikipedia.org/wiki/Affine_transformation
https://zh.wikipedia.org/wiki/分形
原始碼
https://github.com/jayin92/Barnsley-fern
請執行leaves.py