萬有引力定律 vs 庫侖定律
引言
萬有引力定律和庫侖定律分別是力學及電學中重要的定律,我們都知道萬有引力定律是由牛頓歸納出的,而庫侖定律顯然就是由庫侖。萬有引力定律的發表時間約早庫侖定律100年,且這兩條定律都與平方反比定律有關,這篇網誌主要描述這兩條定律,及為了驗證這兩條定律而發展出的實驗。
萬有引力定律
萬有引力定律是由牛頓於1687年出版的《自然哲學的數學原理》首次發表的,他描述了任兩物體之間都會有吸引力,且此吸引力正比於此兩物體質量乘積,反比於兩物體距離平方。
此定律是由牛頓之歸納推理的經驗觀察得出的一般物理規律,若萬有引力定律不是現在這個形式,則太陽系上的行星就不會以橢圓軌道運行了。
但知道其正比關係對實際的計算可說一點用也沒有,因為我們並不能計算出實際的數值,我們需要測量出一個常數,使我們能夠定量的計算出兩物體之間的作用力。
這個常數現在稱為萬有引力常數,代號為G,最早是由物理學及化學家卡文迪西於1797年間接測量出來。
卡文迪西扭秤實驗
卡文迪西被稱作牛頓之後最偉大的科學家之一,因其首次發現庫侖定律及歐姆定律(但都沒有公布),且精確的測量了地球的密度(透過這個實驗我們可以間接算出萬有引力常數G)。
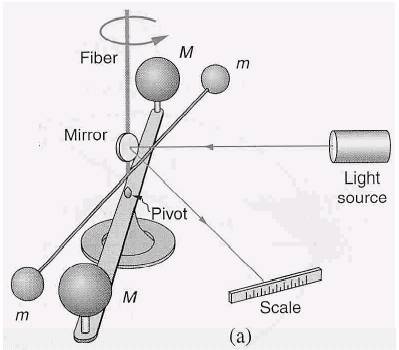
卡文迪西扭秤實驗
卡文迪西是透過一個稱作扭秤的實驗工具,其構造大概長這樣,由兩顆大球、兩顆小球、一條已知扭轉係數的絲線、光源及精準的游標尺所組成的。
因為萬有引力,所以大小球之間就會有一個吸引力,而這個吸引力就會對中間的絲線產生一個力矩,使絲線扭轉,因為絲線本身被扭轉的時候也會產生一個力矩,這個力矩的大小就是此時扭轉的角度乘上此絲線的扭轉係數。直到某個角度時,絲線產生的力矩剛好與萬有引力產生的力矩相等時,木棒就會停止轉動,這時只要測量絲線扭轉的角度,就可以知道萬有引力產生的力矩,進而反推吸引力,我們就可以透過這個數值測量出地球的重量,且因為當時的人已經知道地球的半徑,所以也可以推出密度。
後人用卡文迪西的數據反推萬有引力常數,發現其數值與2014年的數據差距不到1%,可以說是相當精準。
庫侖定律
庫侖定律是由法國物理學家查爾斯·庫侖於1785年發現,其指出了空間中兩個靜止的點電荷,其交互作用力與電量乘積成正比,與其距離平方成反比。
不難發現其形式與牛頓的萬有引力定律形式幾乎相等。
其實在1770年代早期,卡文迪西就利用巧秒的實驗得出了帶電體之間的作用力依賴於帶電量與距離,並得出靜電力與距離的$2\pm \frac{1}{50}$次方成反比,只是卡文迪什沒有公布這個結果。
後來庫侖在1785年使用庫侖扭秤,發現兩點電荷之間的交互作用力也是平方反比定律。
庫侖扭秤

庫侖扭秤(torsion balance)示意圖。庫侖使用扭秤來測量兩個點電荷彼此互相作用的靜電力,因此發現庫侖定律。
庫侖使用庫侖扭秤測量兩點電荷之間的作用力,因而發現庫侖定律。
其原理與卡文迪西的扭秤差不多,在此不再贅述