P vs NP
前言
這篇其實是為了資訊讀書會打的,打完之後發現可以充文章數,所以就把它打進來了。
這篇主要介紹P, NP, NP Complete 和 NP Hard。還有一些已經被證明是NP Complete 的問題。
時間複雜度
就是一個函數,描述一個演算法的執行時間。
簡單來說,假設有一個演算法,你給這個演算法一個大小為n的輸入,它最多要 $6n^3+5n^2+2n+1$ 的時間才能執行完畢,我們就說這個演算法的時間複雜度是$O(n^3)$,這個$O()$我們稱作大O符號 (Big O notation),又叫做漸進符號,它是用另一個(通常更簡單的)函式來描述一個函式數量級的漸近上界。
還有一個東西叫做最壞時間複雜度(Worst-case complexity)記作 $T(n)$
排序演算法的其中一種:插入排序(insertion sort)的時間複雜度是$O(n^2)$,下面是插入排序的Python 程式,為什麼這個演算法的是$O(n^2)$嗎?
def insertionSort(arr):
# Traverse through 1 to len(arr)
for i in range(1, len(arr)):
key = arr[i]
# Move elements of arr[0...i-1],
while j >= 0 and key < arr[j] :
arr[j+1] = arr[j]
j -= 1
arr[j+1] = key
我們今天不會提到太多的排序演算法,因為我們的主題是P vs NP。
P
P 代表的是 Polynomial (多項式),若有一個問題可以在多項式時間(polynomial time)複雜度 ($O(1), O(\log n), O(n^2), O(n \log n), O(n^3), O(n^4)$…皆為多項式時間複雜度)解決,則我們說此問題為P類問題。
最大值問題
給定一個整數集合,求此集合最大值?
這個問題顯然是$O(n)$,所以我們可以說 $\text{maximum problem} \in P$
def maximum(a):
Max = a[0]
for item in a:
if item > Max:
Max = item
return Max
int maximum(int arr[], int len){
max = arr[0];
for(int i = 1;i < len;i++){
if(arr[i] > max){
max = arr[i];
}
}
return max
}
NP
NP 並不是 non-polynomial 的縮寫,而是 non-deterministic (非決定性) polynomial (多項式)。
如果一個問題可以在多項式時間內確定一個解是不是這個問題的解,則我們就說這個問題是NP類問題。
很顯然的,所有$\in$P的問題,一定也$\in$NP,所以P$\subset$NP。
最大值問題
最大值問題顯然$\in$ NP,確定其解的時間複雜度為 $O(n)$
中位數問題
給你一個序列,求其中位數。
這個問題$\in$ P(時間複雜度為$O(n \log n)$),且也 $\in$ NP(時間複雜度為$O(n)$)
NP Hard
NP Hard的非正式定義是:至少和NP中最難的問題一樣難。更正式一點的定義是,如果所有NP問題都可以在多項式時間歸約(Reduction)到某一個問題H,則我們就說問題H是NP Hard (NP 困難)的。
如果一個問題X可以在多項式時間內歸約成問題Y,我們可以記作$X\leq _{P}Y$。所以只要解出問題Y,我們就可以利用這個解去解問題X。
注意一下,NP Hard不一定是NP問題喔。
像等等會提到的子集和加總和3-SAT問題就是NP Hard問題。
NP Complete
若一個問題$\in$NP,且也$\in$NP Hard,這我們稱這個問題為NP完全問題 (NP Complete)。這類問題是最不可能被化簡為P的集合。很多人一開始會把NP的概念與NP Complete概念搞在一起,所以要注意一下。
子集合加總問題
給定一個有限數量的整數集合,找出任何一個此集合的非空子集且此子集內合為零。
暴力法複雜度為$O(2^n)$
DP算法複雜度為$O(n(P-N))$,其中$P$是這個整數集合所有正數的和,$N$為所有負數的和
// Returns true if there is a subset of set[] with sun equal to given sum
bool isSubsetSum(int set[], int n, int sum) {
// The value of subset[i][j] will be true if there is a subset of set[0..j-1]
// with sum equal to i
bool subset[sum+1][n+1];
// If sum is 0, then answer is true
for (int i = 0; i <= n; i++)
subset[0][i] = true;
// If sum is not 0 and set is empty, then answer is false
for (int i = 1; i <= sum; i++)
subset[i][0] = false;
// Fill the subset table in botton up manner
for (int i = 1; i <= sum; i++)
{
for (int j = 1; j <= n; j++)
{
//
subset[i][j] = subset[i][j-1];
if (i >= set[j-1])
subset[i][j] = subset[i][j] || subset[i - set[j-1]][j-1];
}
}
return subset[sum][n];
}
3-SAT
假設有一堆boolean(布林值,可以簡單想成只有1(True)和0(False)的資料型態) $x_1, x_2, x_3, \ldots, x_n$,然後將這些boolean 組成 CNF (Conjunctive Normal Form) 的形式。
$$ \Phi = (x_1 || !x_2 || x_3) \text{ and } (!x_2 || !x_4 || x_5) \text{ and } (x_1 || !x_3 || x_5) \text{ and } (x_2 || x_6 || !x_7) $$
3-SAT 問題就是問說有沒有一種布林值的組合,使得這些由一大堆boolean所組成的CNF的最終結果為True。很顯然我們可以在$O(1)$就可以驗證一組數值是否為3-SAT問題的解,所以它$\in$NP。但我們目前沒有一個演算法可以在多項式時間搞定這個問題,目前唯一的算法只有將所有組合列出來,一個一個帶入原式,這樣的時間複雜度為$O(2^n)$,為指數時間,所以3-SAT問題$\not\in P$,而且我們等等會提到幾個NP問題的例子,我們會發現這些問題都可以在多項式時間歸約到3-SAT問題。
綜合以上3-SAT是一個NP Complete問題。
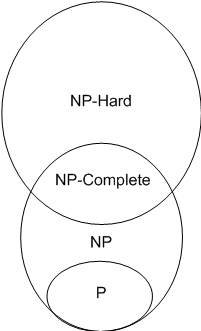
描述P, NP, NP完全,以及NP困難之間關係的歐拉圖
P = NP
P/NP問題是在理論資訊學中計算複雜度理論領域裡至今未被解決的問題,也是克雷數學研究所七個千禧年大獎難題之一。
但這個問題從1971年被史提芬·古克(Stephen A. Cook)和Leonid Levin提出後,到目前仍沒有解答。
剛剛提到的問題有些$\in$NP,但目前暫時$\not\in$P,P=NP問題想要問的就是:是不是所有$\in$NP的問題,都$\in$P,換句話說,P這個集合是否等於NP。
我們剛剛提到NP Complete在這個問題的證明非常有用,因為只要任何一個NP Complete問題被證明出來$\in$P,基本上就能確定P=NP。
很不幸的,現在有一堆問題屬於NP Complete,但沒有一個問題被證明出來$\in$P。
接下來會介紹一些NP問題,還有它怎麼在多項式時間轉換 (歸約) 成3-SAT問題。
CLIQUE 問題
給你一個圖,給定一個數字k,問是否可以在這張圖找到一個子圖,其節點數恰好為k,且為全連接圖。
3-SAT問題可以被歸約成CLIQUE問題,也就是說 3-SAT$\leq _{P}$CLIQUE
Independent Set 問題
給定一個圖,與一個數字$k$,問是否可以找到$k$個不相鄰且相異的點
同樣的,3-SAT問題可以被歸約成Independent Set問題,也就是說 3-SAT$\leq _{P}$ Independent Set
Vertex Cover 問題
給定一個圖,與一個數字k,問是否可以找到k個相異點,使這k個點可以覆蓋到此圖中所有的邊。
同樣的,3-SAT問題可以被歸約成Vertex Cover問題,也就是說 3-SAT$\leq _{P}$ Vertex Cover