證明巴斯卡定理
介紹
大家都知道巴斯卡公式是排列組合中一個十分有用的公式,都叫做巴斯卡公式了,可想而知一定跟巴斯卡三角形有關係
其實巴斯卡三角形也可以被寫成以下形式: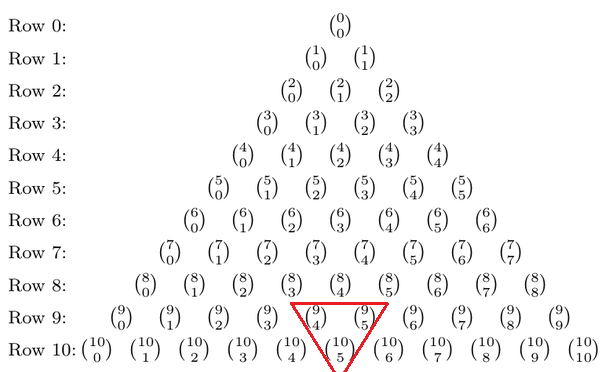
巴斯卡三角形<組合形式>
大家都知道巴斯卡三角形有以下性質:

巴斯卡三角形的性質
於是我們可以利用巴斯卡三角形推導出以下等式:
$$\begin{equation}C_{k}^{n+1} = C_{k-1}^{n}+C_{k}^{n}\end{equation}$$ 舉個例子來說的話就是:
$$C_{5}^{10} = C_{4}^{9}+C_{5}^{9}$$
這個例子可以上面的巴斯卡三角形的組合形式中找到
從結果推導出的證明
組合的定義: $$C_{k}^{n} = \frac{n!}{k!(n-k)!}$$
故(1)可改寫為:
$$\begin{equation}\frac{(n+1)!}{k!(n-k+1)!}=\frac{n!}{(k-1)!(n-k+1)!}+\frac{n!}{k!(n-k)!}\end{equation}$$
開始推導:
$$\frac{(n+1)!}{k!(n-k+1)!}=\frac{n!}{(k-1)!(n-k+1)!}+\frac{n!}{k!(n-k)!}$$ $$(n+1)!=\frac{n!k!}{(k-1)!}+\frac{n!(n-k+1)!}{(n-k)!}$$ $$\frac{(n+1)!}{n!}=\frac{k!}{(k-1)!}+\frac{(n-k+1)!}{(n-k)!}$$ $$n+1=\frac{k!}{(k-1)!}+\frac{(n-k+1)!}{(n-k)!}$$ $$n+1=k+\frac{(n-k)!(n-k+1)}{(n-k)!}$$ $$n+1=k+(n-k+1)$$ $$n+1=n+1$$
等號兩邊相等,故巴斯卡公式成立。
但是我認為這個證法不夠精確,我已經先假設巴斯卡公式成立再去證明它的確成立,正確的證法應該要從源頭來下手。
從源頭推導出巴斯卡公式
我認為這個證明有點曲折,希望有更好的證法
$$原式=C_{k-1}^{n}+C_{k}^{n}$$ $$=\frac{n!}{(k-1)!(n-k+1)!}+\frac{n!}{k!(n-k)!}$$ $$=\frac{n!}{\frac{k!}{k}(n-k)!(n-k+1)}+\frac{n!}{k!(n-k)!}$$ $$=\frac{n!k}{k!(n-k)!(n-k+1)}+\frac{n!}{k!(n-k)!}$$ $$=\frac{n!}{k!(n-k)!}(\frac{k}{n-k+1}+1)$$ $$=\frac{n!}{k!(n-k)!}(\frac{k+(n-k+1)}{n-k+1})$$ $$=\frac{n!}{k!(n-k)!}(\frac{n+1}{n-k+1})$$ $$=\frac{n!(n+1)}{k!(n-k)!(n-k+1)}$$ $$=\frac{(n+1)!}{k!((n+1)-k)!}$$ $$=C_{k}^{n+1}$$