證明 Second (Partial) Derivative Test
Second (Partial) Derivative Test
Let $f : D \rightarrow \mathbb{R}$ be a function in two variables $x$ and $y$. Suppose that $f, f_{x}, f_{y}, f_{xx}, f_{yy}, f_{xy}, f_{yx}$ are all continuous in an open disk centered at $(a, b)$ and $f_{x}(a, b) = f_{y}(a, b) = 0$. (Then $f_{xy}(a, b) = f_{yx}(a, b)$)
Let
$$D(x, y) = f_{xx}(x, y) f_{yy}(x, y) - \left(f_{xy}(x, y)\right)^{2}$$
Then
- if $D(a, b) > 0$ and $f_{xx}(a, b) > 0$, then $f(a, b)$ is a local minimum of $f$,
- if $D(a, b) > 0$ and $f_{xx}(a, b) < 0$, then $f(a, b)$ is a local maximum of $f$,
- if $D(a, b) < 0$, then $(a, b)$ is saddle point of $f$,
- if $D(a, b) = 0$, no conclusion.
$D(x, y)$ is called the Discriminant or Hessian of $f$.
Proof of Second (Partial) Derivative Test
Let $\vec{u} = <u_{1}, u_{2}>$ be any unit vector in $\mathbb{R}^{2}$. Let $\delta$ be a positive number such that $f, f_{x}, f_{y}, f_{xx}, f_{yy}, f_{xy}, f_{yx}$ are all continuous in $U_{\delta}(a, b)$.
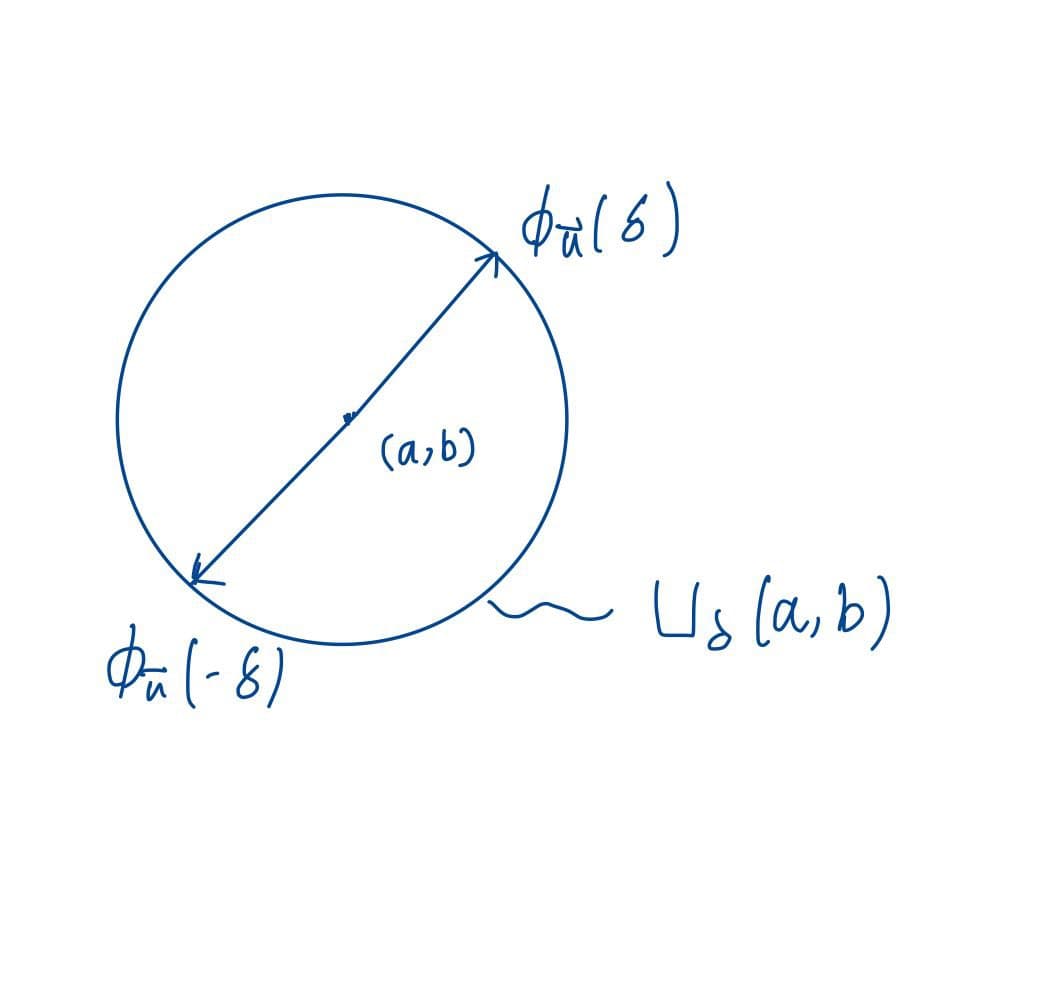
Graph of $U_{\delta}(a, b)$, $\phi_{\vec{u}}(\delta)$ and $\phi_{\vec{u}}(-\delta)$
Define
$$\phi_{\vec{u}}(t) = f_{x}(a+tu_{1}, b+tu_{2})$$, where $t \in (-\delta, \delta)$.
By the Chain Rule, one has
$$\phi’{\vec{u}}(t) = f{x}(a+tu_{1}, b+tu_{2})\cdot u_{1} + f_{y}(a+tu_{1}, b+tu_{2}) \cdot u_{2}$$
So
$$\phi’{\vec{u}}(0) = f{x}(a, b)\cdot u_{1} + f_{y}(a, b) \cdot u_{2}=0$$
Hence $(a, b)$ is a critical point of $f$, therefore $f_{x}(a,b)=f_{y}(a,b)=0$.
Use The Chain Rule again, one has
$$\phi’’{\vec{u}}(t) = f{xx}(a+tu_{1}, b+tu_{2}) \cdot u_{1}^2 + f_{yy}(a+tu_{1}, b+tu_{2}) \cdot u_{2}^{2} \ + 2f_{xy}(a+tu_{1}, b+tu_{2}) \cdot u_1 u_2$$
So
$$\phi’’{\vec{u}}(0) = f{xx}(a, b) \cdot u_{1}^2 + 2f_{xy}(a, b) \cdot u_1 u_2 + f_{yy}(a, b) \cdot u_{2}^{2} = 0$$
Observe that $-4D(a, b) = 4f^2_{xy}(a, b) - 4 f_{xx}(a, b) f_{yy}(a, b)$ is the discriminant of the quadratic polynomial $Q(X) = f_{xx}(a, b) X^2 + 2f_{xy}(a, b) X + f_{yy}(a, b)$.
And we know that
$$\frac{\phi’’{\vec{u}}(0)}{u_2^{2}} = f{xx}(a, b) \cdot \left(\frac{u_{1}}{u_2}\right)^2 + 2f_{xy}(a, b) \cdot \left(\frac{u_1}{u_2}\right) + f_{yy}(a, b)$$
which is equal to $Q(\frac{u_1}{u_2})$ (if $u_2 = 0$, we can divide $u_1$ instead, because $\vec{u}$ is a unit vector, $u_1u_2 \neq 0$).
So if the discriminant of $Q$, $-4D(a, b) < 0$, it indicates $Q$ have no root. Then we can tell $Q$ is always positive or negative by its leading coefficient $f_{xx}(a, b)$. If $f_{xx}(a, b) > 0$, then $Q$ is always postive. If$f_{xx}(a, b) < 0$, then $Q$ is always negative.
In conclusion, we have
- Suppose $D(a, b) > 0$ and $f_{xx}(a, b) > 0$. Then one has $\phi’’_{\vec{u}}(0) > 0$ for all $\vec{u}$. Therefore, f(a, b) is a local minimum.
- Suppose $D(a, b) > 0$ and $f_{xx}(a, b) < 0$. Then one has $\phi’’_{\vec{u}}(0) < 0$ for all $\vec{u}$. Therefore, f(a, b) is a local maximum.
- Suppose $D(a, b) < 0$. Then one has $$\phi^{\prime\prime}{\vec{u}}(0) > 0$$ for some $\vec{u}$ and has $\phi^{\prime\prime}{\vec{u}}(0) < 0$ for some $\vec{u}$. Therefore, $(a, b)$ is saddle point of $f$.
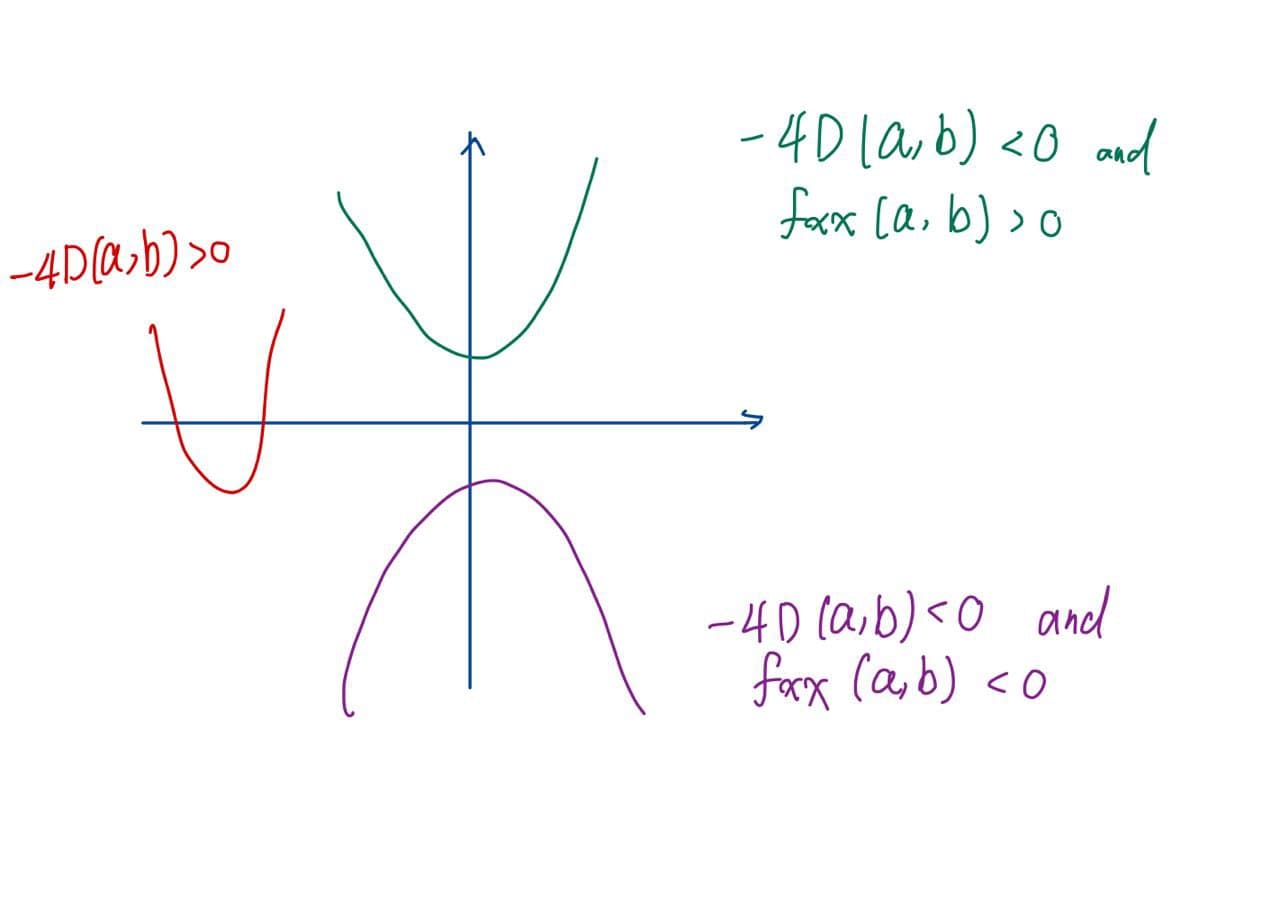
Credit
- 中央大學微積分講義